
The third term of the arithmetic progression is 5. The first, second and fifth terms of an arithmetic progression are the first three terms of a geometric progression.
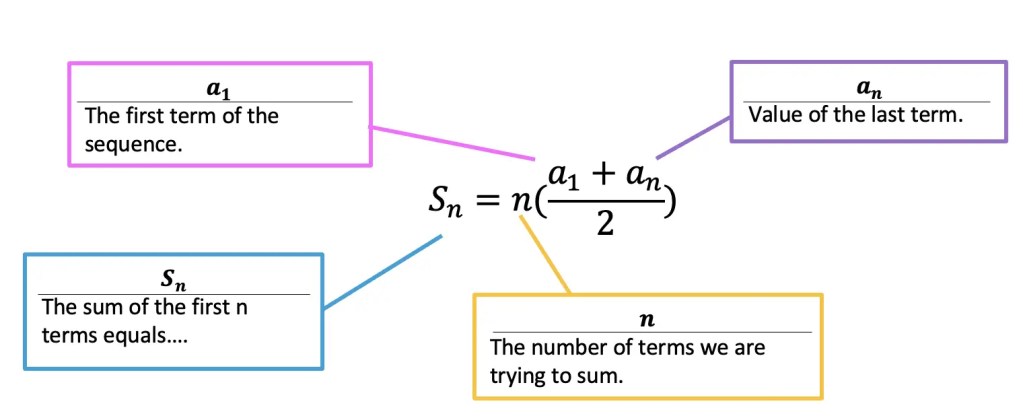
So every time you add another term to the above sequence, the result gets closer and closer to 1. Therefore, the sum to infinity is 0.5/0.5 = 1. This value is equal to:įind the sum to infinity of the following sequence: 1 In other words, if you keep adding together the terms of the sequence forever, you will get a finite value. In geometric progressions where |r| < 1 (in other words where r is less than 1 and greater than –1), the sum of the sequence as n tends to infinity approaches a value. The sum to infinity of a geometric progression What is the sum of the first 5 terms of the following geometric progression: 2, 4, 8, 16, 32 ? S n(1 – r) = a – ar n (since all the other terms cancel)Īnd so we get the formula above if we divide through by 1 – r. The sum of the first n terms of a geometric progression is: The nth term of a geometric progression, where a is the first term and r is the common ratio, is:įor example, in the following geometric progression, the first term is 1, and the common ratio is 2: r is known as the common ratio of the sequence. the first 20 odd numbers).Ī geometric progression is a sequence where each term is r times larger than the previous term. Sum the first 20 terms of the sequence: 1, 3, 5, 7, 9. You may need to be able to prove this formula. The sum to n terms of an arithmetic progression U n = 3 + 2(n - 1) = 2n + 1, which we already knew. In general, the nth term of an arithmetic progression, with first term a and common difference d, is: a + (n - 1)d. The terms in the sequence are said to increase by a common difference, d.įor example: 3, 5, 7, 9, 11, is an arithmetic progression where d = 2. In the above example, U r = 3r + 2 and n = 3.Īn arithmetic progression is a sequence where each term is a certain number larger than the previous term. up to and including n in turn for r in U r.

For the sequence U r, this means the sum of the terms obtained by substituting in 1, 2, 3. Now add up all of the term that you have written down. Keep doing this until you get to 4, since this is the number above the S. Then replace r by 2 and write down what you get. This means replace the r in the expression by 1 and write down what you get. The Greek capital sigma, written S, is usually used to represent the sum of a sequence. , the sum to 3 terms = S 3 = 2 + 4 + 6 = 12.
Arithmetic and geometric sequences formulas sum series#
The series of a sequence is the sum of the sequence to a certain number of terms.


 0 kommentar(er)
0 kommentar(er)
